4  Practical examples

4.3  Securing against sliding in the longitudinal direction with slack tie-down lashing

This example is intended to demonstrate that a tolerable cargo movement may re-establish the securing effect in the longitudinal direction of a transverse tie-down lashing, even if the pretension has first completely disappeared due to settling of the cargo.

Three loaded pallets each of a mass of 1.0 t are placed side by side on the loading area and are tied down with two belts. The dimensions of the units are 1200 x 800 x 1200 mm. The complete package has a height h of 1.2 m and a breadth b of 2.4 m.

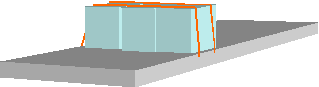
Figure 19: Tie-down lashing of box pallets

The belts run virtually vertically on the external sides. At the beginning of the journey, the belt pretension amounts on average to around F₀ = 2 kN. The coefficient of friction relative to the loading area is assumed to be m = 0.38 and that between the belts and cargo to be m_L = 0.25. This example solely investigates securing against forward sliding.

The external force is determined as conventionally agreed.

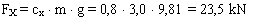
Conventional assessment of the securing against forward sliding:

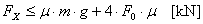
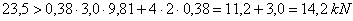
According to the conventional assessment, securing is not adequate, with a shortfall of just about 40%.

Taking account of cargo movement:

In order to simplify the following presentation, it is assumed that the pretension has declined to zero by the three pallets having moved closer to one another. If the cargo is permitted to shift forward in the event of an extreme load, belts on the top of the cargo are dragged along without slipping until an equilibrium is reached between the longitudinal component of the belt force F_X and friction on the top of the cargo F_Z × m_L. The resultant maximum movement distance is calculated:

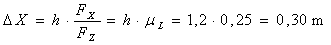
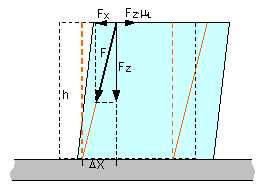
Figure 20: Cargo sliding and racking by DX in the longitudinal direction

This distance may be made up of the sliding of the pallets and shear deformation. The belts have lengthened in this state by the amount DL.

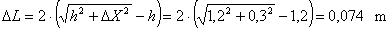
Lengthening results in force being developed, but this is not uniformly distributed over the length of the belt. The horizontal central part maintains a force which is reduced pro rata with Euler’s friction losses at the edges relative to the force in the external parts of the belt.

Each belt has an LC = 25 kN and an elongation of 3.5% when LC is reached. The spring constant of the vertical parts of the belt amounts to D_v = DF / DL = 25 / (0.035 × 1.2) = 595 kN/m, that of the horizontal parts of the belt only D_h = DF / DL = 25 / (0.035 × 2.4) = 298 kN/m. On this basis, the individual changes in length, which must add up to the total change in length DL, may be determined with the initially unknown force F in the external parts of the belt.

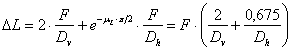
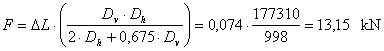
The belts thus reach a force in the external parts of a good 13 kN on both sides. The horizontal central parts just about reach 9 kN. The longitudinal and vertical components of the external forces are calculated for the sliding balance.

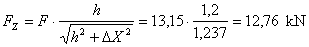
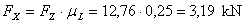
These values are used to make up a sliding balance.

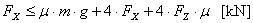
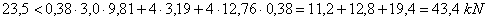
The balance is amply met with a surplus of just about 85%. The cargo will in fact thus not have to slide or distort over the entire 30 cm in order to reach an equilibrium of forces. This example is an impressive demonstration of the securing potential which can be obtained from limited cargo movement. The question as to whether the middle unit remains secured by friction relative to the other two external units and to the loading area is left unanswered here.