4  Practical examples

4.4  Securing against sliding in the transverse direction by slack tie-down lashing

This example is intended to demonstrate that a tolerable cargo movement may also reestablish the securing effect of slackened tie-down lashings in the transverse direction. The same circumstances as in the preceding example are used for this purpose.

The external force is determined as conventionally agreed.

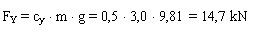
Conventional assessment of the securing against sideways sliding:

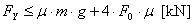
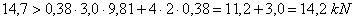
According to the conventional assessment, securing is not adequate, with a shortfall of a good 3%. Here too it is subsequently assumed that the pretension F₀ in the tie-down lashing has been lost due to the cargo units moving closer together.

Unlike in the preceding example, where the movement distance selected was the DX value at which the belts still just grip the surface of the cargo by friction, in this example the movement distance DY to be assumed was to be determined on the basis of the geometric conditions of the loading area.

The cargo package has a breadth of 2.4 m. At an assumed net breadth of the loading area of 2.5 m and with initially central loading, the pallets may slip by 5 cm to the side before coming into contact with the sidewalls. Racking (shear deformation) is additionally assumed, in which the upper edges of the units are pulled a further 10 cm to the side.

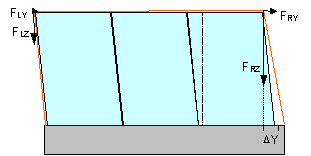
Figure 21: Cargo sliding and racking DY in Querrichtung

The lengthening of the belts arising from these movements is calculated:

Initial length of the external parts of the belt:	m
New length on the right:	m
New length on the left:	m
Change in length:	m

This change in length results in force being created in the belt, which is distributed such that the force F_R acts in the right-hand vertical part of the belt, while forces reduced by Euler’s friction losses act in the horizontal central part and the left-hand vertical part. The individual changes in length must again correspond to the total change in length. Change of direction on the right amounts to a = 81° = 1.40 rad, while change of direction on the left amounts to b = 95° = 1.66 rad. The coefficient of friction m_L = 0.25 applies as in the preceding example.

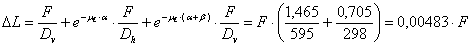
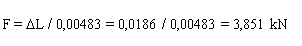
F_R = 3,851 kN with F_RY = 0,60 kN and F_RZ = 3,80 kN accordingly acts in the right-hand part of the belt

F_L = 0,465 × F_R =1,791 kN with F_LY = 0,16 kN and F_LZ = 1,78 kN acts in the left-hand part of the belt

The balance is completed with these values:

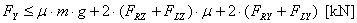
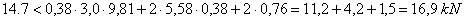
The balance is achieved with a surplus of 15%, any possible retention forces arising from the edge of the loading area having been disregarded. This example confirms that a slight cargo movement can compensate the complete loss of pretension. However, it must not be concluded on this basis that pre-tensioning is unimportant. Instead, the actual, more probable mode of action of a tie-down lashing should be pointed out, which does not correspond to that represented in the conventional approach to calculation. The conventional approach to calculation clearly does not adequately model the physics to be applied in this case.

It is not yet possible to state the extent to which the conventional approach to calculation may need to be modified on this basis.