2  Direktsicherung

Direktsicherung von Ladung auf einem Fahrzeug bezeichnet alle Methoden, die als Hauptwirkmechanismus eine „formschlüssige“ Kraftübertragung zwischen Ladung und Fahrzeug nutzen. Das ist der wesentliche Gegensatz zur Reibungssicherung (Niederzurrung), die als Hauptwirkmechanismus eine „kraftschlüssige“ Verbindung zwischen Ladung und Fahrzeug, also Reibung nutzt, die durch die Niederzurrung nur ein wenig verstärkt wird.

Während die Wirkung formschlüssiger Kraftübertragungen von der Festigkeit des Sicherungsmaterials begrenzt wird, sind der Reibung engere Grenzen gesetzt, die nur marginal vom Sicherungsmittel beeinflusst werden. Deshalb kann eine Direktsicherung um rund eine Zehnerpotenz leistungsfähiger sein als eine Reibungssicherung aus gleichwertigem Material.

Beispiel: Ein direkt sichernder Gurt kann bis zu seiner zulässigen Belastbarkeit LC von beispielsweise 2500 daN belastet werden. Der gleiche Gurt als Niederzurrung eingesetzt und mit der genormten Vorspannkraft S_TF von 400 daN gespannt, liefert bei einem Reibbeiwert μ = 0,3 eine Sicherungswirkung von höchstens 2 × 0,3 × 400 = 240 daN.

Wird der direkt sichernde Gurt mit einer Winkelabweichung von der Richtung der gewünschten Sicherungswirkung angebracht, so ist seine Sicherungswirkung geringer. Das wird in den Rechenmodellen der angeführten Richtlinien und Normen ziemlich einheitlich berücksichtigt.

Rechnerisch wird aber in keiner der Vorgaben in Betracht gezogen, dass die jeweils mögliche Sicherungswirkung nur bei einer merklichen Ladungsbewegung erreicht wird, die bei ungünstigen Zurrwinkeln sogar gefährlich groß werden kann. Es wird lediglich in der Norm DIN EN 12195-1:2011 mit Hinweis auf die notwendige Ladungsbewegung die Verwendung eines um 25% verringerten Reibbeiwerts in den Kräftebilanzen quer und längs zum Fahrzeug gefordert. Dieser kann als Gleitreibbeiwert aufgefasst werden.

Diese Abhängigkeit der Wirkung einer Direktsicherung von Ladungsbewegung hat außerdem zur Folge, dass „im Verbund“ eingesetzte, direkt wirkende Sicherungsmittel nur dann mit ihrer zulässigen Belastbarkeit LC wirken können, wenn sie gleiche elastische Eigenschaften in Bezug zur Richtung der Ladungsbewegung haben. Diese einschränkenden Begleitumstände der Direktsicherung werden in den folgenden Kapiteln näher erklärt und exemplarisch dargestellt.

2.1 Notwendige Ladungsbewegung

Das Hooke’sche Gesetz sagt aus, dass alle festen Körper, und dazu zählen auch Ladungssicherungsmittel, sich verformen müssen, wenn sie eine Kraft übertragen sollen. Diese Verformung bedeutet für ein Zurrmittel Dehnung und für ein Blockiermittel Stauchung. Wenn diese Verformungen im zulässigen Bereich bleiben, dann sind sie elastisch. Das bedeutet, es gibt keine bleibende Verformung und der Vorgang einer Kraftübertragung kann beliebig oft wiederholt werden. Genau das erwartet man von einem Ladungssicherungsmittel.

Das Hooke’sche Gesetz sagt ferner aus, dass für praktische Anwendungen im unteren Lastbereich die Lastaufnahme und die zugehörige Formänderung zueinander proportional sind. Das erleichtert alle Berechnungen. Für metallische Zurrmittel trifft diese Annahme recht gut zu, für Kunstfasergurte weniger, aber immer noch ausreichend (siehe Bild 17). Auch für Holz als Blockiermittel kann diese Annahme bei Kurzzeitbelastung verwendet werden.

Zur Ermittlung der zur Kraftübertragung notwendigen Ladungsbewegung wird auf der Grundlage des Hooke’schen Gesetzes, wie bereits in Kapitel 1.4.3 gezeigt, der Begriff der Federkonstanten verwendet. Die Federkonstante D erlaubt eine einfache Umrechnung von Längenänderung ΔL in Kraftänderung ΔF und umgekehrt nach Gleichung (26):

Wie schon in Kapitel 1.4.3 erläutert, ist es sinnvoll, zunächst die nominelle Federkonstante D_N zu verwenden, die unabhängig von der Länge des Sicherungsmittels nur von seinem Querschnitt und einer Materialkonstanten abhängt. Es gilt nach Gleichung (27):

und nach Gleichung (28):

Damit lassen sich unter Annahme von 4% elastischer Dehnung von Zurrgurten und 1,5% elastischer Dehnung von Ketten, jeweils bei Erreichen von LC, folgende Werte für nominelle Federkonstanten in daN bestimmen:

2.1.1 Zurrmittel

Direkt sichernde Zurrmittel werden vom Sicherungspunkt an der Ladungseinheit zum Sicherungspunkt am Fahrzeug gespannt. Dabei treten je nach den Gegebenheiten Abweichungen von der Idealrichtung des Zurrmittels auf, die in Richtung der zu übertragenden Kraft liegen sollte. Die dadurch entstehende Zurrgeometrie nimmt einen erheblichen Einfluss auf die zur Kraftübertragung notwendige Ladungsbewegung.

Bild 33 zeigt einen Lasching der Länge L, der unter einem vertikalen Winkel α zur Ladefläche verläuft. Außerdem weicht der Lasching um den horizontalen Winkel β_x von der Längsrichtung des Fahrzeugs ab. Die gleichzeitige Abweichung von der Querrichtung des Fahrzeugs wird durch den horizontalen Winkel β_y dargestellt.

Neben dieser auf Winkeln beruhenden Beschreibung der Zurrgeometrie besteht die gleichwertige Möglichkeit, den Lasching durch seine geometrischen Komponenten X, Y und Z zu beschreiben. Diese Möglichkeit führt zu etwas übersichtlicheren Formeln und wird im folgenden vorzugsweise benutzt.

Bild 33: Geometrie einer Direktzurrung

Für die genannten Komponenten X, Y und Z sowie die Länge L des Laschings gilt der räumliche Satz des Pythagoras (L ist die räumliche Diagonale im Quader mit den Seiten X, Y, Z):

Der Lasching wird mit der Vorspannung F_T festgesetzt. Um die zulässige Belastung LC zu erreichen, muss er sich um den Betrag ΔL dehnen. Es gilt:

Rutschen der Ladung

Bei einem Lastfall in x-Richtung muss sich die Ladungseinheit um die Strecke ΔX bewegen, um die Längenänderung ΔL zu bewirken. Nach Pythagoras erhält man:

Bei einem Lastfall in y-Richtung muss sich die Ladungseinheit um die Strecke ΔY bewegen.

Gleichung (55) zeigt, dass man die Längenänderung ΔL gering halten kann, indem man bei gegebener zulässiger Belastung LC eine hohe Vorspannung F_T aufbringt, die Länge L des Laschings möglichst klein macht und/oder ein Material mit großer nomineller Federkonstante wählt, also z.B. eine stählerne Kette anstatt eines Kunstfasergurts.

Die Gleichungen (56) und (57) lassen sich so umformen, dass eine Abschätzung des Verhältnisses von Ladungsbewegung zu Längenänderung möglich ist. Die Umformungen lauten:

Zieht man in Betracht, dass die beiden addierten Änderungswerte klein gegenüber den zweifachen Grundwerten sind, so kann man mit ausreichender Genauigkeit schreiben:

Die Ladungsbewegungen sind also im Regelfall immer größer als die Längenänderungen, niemals kleiner. Sie können nur dann auf die Größe der Längenänderungen beschränkt werden, wenn der Lasching ausschließlich in x-Richtung bzw. in y-Richtung geführt wird, also keine sonstigen Komponenten hat. Wenn jedoch X bzw. Y nahe oder gleich Null ist, was ohnehin als äußerst ungünstige Anordnung anzusehen ist, liefern die Näherungsgleichungen (59) keine richtigen, sondern zu große Ergebnisse. Die Berechnung von ΔX bzw. ΔY mit den Gleichungen (56) und (57) ist daher grundsätzlich vorzuziehen.

Beispiel: Zur Demonstration der Größenordnungen, um die es hier geht, wird ein einfaches Beispiel durchgerechnet. Ein Lasching wird ähnlich wie in Bild 33 gesetzt mit den Längenkomponenten X = 1,4 m, Y = 2,0 m, Z = 1,3 m. Die Länge des Laschings beträgt:

Der Lasching ist ein einfach gelegter Zurrgurt mit LC = 2500 daN. Er ist auf S_TF = 400 daN vorgespannt. Die zum Erreichen von LC notwendige Längenänderung beträgt:

Bei Beanspruchung in x-Richtung ist die notwendige Ladungsbewegung nach Gl. (56):

Bei Beanspruchung in y-Richtung ist die notwendige Ladungsbewegung nach Gl. (57):

Beide Ergebnisse sind noch nicht extrem, zeigen aber, dass die notwendige Ladungsbewegung für eine Direktsicherung mit Gurten erheblich sein kann.

Kippen der Ladung

Eine Ladungseinheit, die eher kippt als rutscht, muss um einen kleinen Winkel Δδ ankippen, um die zur vollen Lastaufnahme des Laschings erforderliche elastische Dehnung zu erzeugen. Auch hier kann ein einfacher Zusammenhang zwischen dieser Längenänderung und dem Ankippwinkel gefunden werden.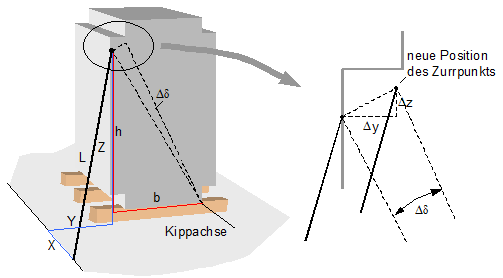

Bild 34: Direktsicherung gegen Kippen

Da der Ankippwinkel klein ist, kann die neue Position des Zurrpunkts an der Ladungseinheit mit einem vereinfachenden Ansatz gefunden werden.

Der räumliche Satz des Pythagoras führt zum gewünschten Zusammenhang zwischen ΔL und Δδ für ein Ankippen in Querrichtung des Fahrzeugs.

Nach weiteren Umformungen und zulässigen Vereinfachungen erhält man:

Beispiel: Zur Demonstration der Größenordnungen wird ein einfaches Beispiel durchgerechnet. Ein Lasching wird ähnlich wie in Bild 34 gesetzt mit den Längenkomponenten X = 0,9 m, Y = 0,7 m, Z = 2,0 m. Die Länge des Laschings beträgt:

Der Lasching ist ein einfach gelegter Zurrgurt mit LC = 2500 daN. Er ist auf S_TF = 400 daN vorgespannt. Die zum Erreichen von LC notwendige Längenänderung beträgt:

Die Abstände zur Kippachse sind h = 1,9 m und b = 1,2 m. Damit erhält man den Ankippwinkel nach Gleichung (60).

Das Ankippen von 2,7° bewirkt z.B., dass sich die Ladungseinheit auf der Seite gegenüber der Kippachse um knapp 6 cm anhebt.

2.1.2 Blockierung

Blockierungen werden auf Druck beansprucht. Da eine schräge Kraftübertragung zum seitlichen Wegsprengen der Blockierung führen könnte, werden sie üblicherweise so angebracht, dass sie genau in Richtung der Belastung wirken. Das vereinfacht die Betrachtung der notwendigen Ladungsbewegung. Sie ist genau so groß, wie die Längenänderung der Blockierung, genauer, wie der Betrag, um den sie zusammengedrückt werden muss, um die Druckkraft nach dem Hooke’schen Gesetz zu übertragen.

Blockierungen auf Straßenfahrzeugen setzen sich zusammen aus dem begrenzenden Element der Ladefläche, also elastischer Stirnwand, Bordwand, Runge oder Spezialaufbau, und den ausfüllenden Elementen, meist Holzbohlen, Paletten oder sogar Luftpolster. Dadurch ist es schwer, eine halbwegs verlässliche Federkonstante zu bestimmen, die es ermöglicht, die Formänderung aus der Blockierkraft abzuschätzen. Hinzu kommt, dass viele Blockierungen am Beginn einer Fahrt selten bereits vollen Kontakt haben, so dass im Falle einer Belastung zunächst ein gewisser „Leerlauf“ erfolgt, bevor die blockierende Gegenkraft aufgebaut wird. Dieser Leerlauf sollte so klein wie möglich gehalten werden, um zu verhindern, dass die bewegte Ladung zuviel kinetische Energie aufnimmt.

Trotz dieser Unsicherheiten kann davon ausgegangen werden, dass eine gezielt hergestellte Blockierung, z.B. mit Holzbohlen zur Stirnwand, im Auslegungslastfall nur wenige Zentimeter an Bewegung der Ladung benötig bzw. zulässt, um die volle Last zu übernehmen, also viel weniger als dies bei Laschings überwiegend der Fall ist.

2.2 Zulässige Vorspannung einer Direktzurrung

Direktzurrungen sollten grundsätzlich zweiseitig angeordnet werden, so dass Sicherungswirkung nach vorn und hinten bzw. nach rechts und links ermöglicht wird. Wird überall eine Vorspannkraft aufgebracht, so besteht die Sicherungswirkung im Ruhezustand der üblicherweise schrägen Zurrungen lediglich aus der Reibungserhöhung zwischen Ladung und Ladefläche, die durch die Vertikalkomponenten der Vorspannkräfte erzeugt wird. Die Horizontalkomponenten der Vorspannkräfte heben sich weitgehend gegenseitig auf. Damit unterscheidet sich die Direktzurrung zunächst nicht von einer Niederzurrung.

Die volle Belastbarkeit LC der Zurrmittel kommt erst zur Wirkung, wenn die Ladung durch eine äußere Kraft – meist Trägheitskraft bei Bremsmanöver oder Kurvenfahrt – so weit fortbewegt oder verformt worden ist, dass auf der belasteten Seite die Kraft in den Zurrmitteln durch deren Längung von der Vorspannkraft auf die Zurrkraft LC ansteigt und auf der Gegenseite durch Verkürzung auf Null abfällt. Nur unter dieser Voraussetzung gelten die in Richtlinien und Normen üblichen Rechen­modelle für die Bemessung einer Direktzurrung. Diese Modelle gehen stets davon aus, dass die Zurrkraft auf der Gegenseite gleich Null ist.

Diese Voraussetzung wird in der Praxis meist ohne Schwierigkeiten erreicht. Wichtig ist dabei die Höhe der anfänglichen Vorspannkraft auf beiden Seiten. Beträgt diese z.B. 50% des Wertes von LC und ist die Anordnung der Zurrmittel auf beiden Seiten symmetrisch und von gleicher Elastizität, so wird dieser Idealzustand gerade erreicht. Bei höherer Vorspannung würde auf der Gegenseite eine (schädliche) Restkraft verbleiben oder auf der belasteten Seite würde der LC-Wert überschritten. Damit ist eine Vorspannkraft von 50% LC für mechanisch symmetrische Anordnungen der Grenzfall. Darauf wird z.B. in der Richtlinie VDI 2702 ausdrücklich hingewiesen.

Für asymmetrische Anordnungen sinkt diese Grenze. Eine einfache Faustregel kann hierfür nicht gegeben werden. Ein Beispiel soll diese Situation erläutern.

Beispiel: Eine Ladungseinheit ist nach vorn und hinten mit über Kreuz laufenden Gurten von zulässiger Belastung LC = 1000 daN und Vorspannung F_T = 500 daN gesichert. Die Geometrie der Gurte ist:

Bild 35: Asymmetrische Direktzurrung

Wenn die volle Belastbarkeit LC von den beiden hinteren Gurten bei einer Vollbremsung verlangt wird, so müssen sie sich um ΔL dehnen.

Diese Dehnung wird durch eine Verlagerung der Ladungseinheit um die Strecke ΔX erreicht.

Durch diese Verlagerung verkürzen sich die vorderen Gurte um ΔL.

Diese Verkürzung verringert die Vorspannkraft in den vorderen Gurten um ΔF.

Da die vorderen Gurte mit 500 daN vorgespannt waren, haben sie immer noch eine Spannkraft von 352 daN, wenn die hinteren Gurte bereits ihre zulässige Belastung LC erreicht haben. Dadurch wird deren Sicherungswirkung in der Horizontalkomponente vermindert. Diese Verminderung wird aber abgemildert oder sogar aufgehoben, weil die Vertikalkomponenten der vorderen Gurte über den Reibbeiwert zwischen Ladung und Ladefläche positiv zur Sicherung beitragen. Die Gesamtsicherungswirkung dieser asymmetrischen Anordnung wird im folgenden Kapitel berechnet.

Eine Vorspannkraft von 50% der zulässigen Belastung wird bei Zurrgurten nur selten erreicht und diese Vorspannkraft fällt durch Setzvorgänge schon nach kurzer Zeit etwas ab. Somit tritt das Problem einer übermäßigen Vorspannkraft bei Gurten kaum auf. Bei Zurrketten mit hochwertigen Spannvorrichtungen ist ein übermäßiges Vorspannen mit bestimmten, unzulässigen Hilfsmitteln möglich und muss unbedingt vermieden werden. Der Ratschlag in Broschüren von Herstellern, Kettenlaschings nur „handfest“ vorzuspannen, sollte jedoch nicht so verstanden werden, dass die Ketten „lose“ gefahren werden sollen. Auch für Ketten gilt die optimale Grenze der Vorspannkraft von 40% bis 50% der zulässigen Belastung LC.

2.3 Sicherungswirkung einer Direktzurrung

2.3.1 Wirkung gegen horizontale Bewegung (Versatz, Verschub)

Die Sicherungswirkung einer Direktzurrung gegen horizontale Kräfte besteht wie bei Niederzurrungen aus den Teilwirkungen der Horizontalkomponente und der auf Straßenfahrzeugen stets nach unten gerichteten Vertikalkomponente der Zurrkraft, die so über die Reibungserhöhung sichernd wirkt. Während bei Niederzurrungen die Reibungserhöhung dominiert, sollte man bei Direktsicherungen mit einem möglichst kleinen Zurrwinkel α dafür sorgen, dass die ergiebigere Wirkung der Horizontalkomponente gut genutzt wird (Bild 36 links).

Es besteht in allen Richtlinien und Normen Einigkeit darüber, dass als Reibbeiwert für die Direktzurrung der Gleitreibbeiwert verwendet werden soll, weil die Wahrscheinlichkeit groß ist, dass die Ladung zum Erreichen der vollen Sicherungswirkung gleiten muss, wie in den vorangehenden Kapiteln erläutert worden ist. Die Sicherungswirkung einer Direktzurrung gegen Versatz einer Ladungseinheit wird durch folgende Gleichungen beschrieben:

Zu beachten ist, dass für eine exakte Berechnung in beiden Gleichungen die um die kleinen Gleitstrecken ΔX bzw. ΔY vergrößerten Horizontalkomponenten und auch die um ΔL vergrößerte Länge L eingesetzt werden. Das wird in allen üblichen Rechenmodellen nicht gemacht. Statt dessen werden stets die Ausgangswerte X, Y und L verwendet, weil die Ladungsbewegung insgesamt ignoriert wird. Die Ergebnisse liegen dadurch jedoch stets auf der sicheren Seite. Bei kleinen Ausgangswerten von  X bzw. Y, also ohnehin ungünstigen Sicherungsgeometrien, sind die Abweichungen der üblichen Rechenmodelle von den Ergebnissen der Gleichungen (61) und (62) allerdings erheblich. Die vereinfachten Rechenmodelle sind in dieser Hinsicht für Kräftebilanzen angemessen und brauchbar.

An dieser Stelle wird die Sicherungswirkung für das Beispiel des vorangegangenen Kapitels mit einem Gleitreibbeiwert μ_D = 0,3 berechnet.

Der konventionelle Rechenansatz ergibt für die gleiche Situation folgendes Resultat:

Damit weicht das Ergebnis in diesem Beispiel um knapp 6% zur sicheren Seite vom Ergebnis einer genaueren Berechnung ab. Nicht berücksichtigt ist in dieser Beurteilung die Dynamik sich bewegender Ladung, die zu einem etwas erhöhten Sicherungsbedarf führt.

Bild 36: Sicherungswirkungen gegen Rutschen und Kippen

2.3.2 Wirkung gegen Kippen

Die Sicherungswirkung einer Direktzurrung gegen Kippen setzt sich ebenfalls aus den Teilwirkungen der Horizontalkomponente und der Vertikalkomponente der Zurrkraft zusammen. Eine exakte Berechnung sollte das mögliche Ankippen und die dadurch auftretenden Änderungen der wirksamen Kräfte und Hebel berücksichtigen. Die Gleichung für die Sicherungswirkung in Querrichtung des Fahrzeugs lautet mit den Größen in Bild 36 rechts:

Zum Vergleich wird das übliche, vereinfachte Modell wiedergegeben.

Die Unterschiede in den Ergebnissen sind meist vernachlässigbar klein. Allerdings weichen die Ergebnisse der vereinfachten Modelle zur unsicheren Seite ab. Sie sind stets etwas größer als die genaueren Ergebnisse. Die vereinfachten Rechenmodelle für Kippbilanzen sind dennoch angemessen und brauchbar.

Die Sicherungswirkung einer Direktzurrung gegen Kippen in Längsrichtung wird nach Gleichung (63) sinngemäß berechnet.

In Bild 36 rechts ist zu beachten, dass der Wert von b im gewählten Beispiel negativ ist. (b = horizontaler Abstand des Zurrpunkts an der Ladungseinheit von der Kippachse). Die Vertikalkomponente der Zurrkraft unterstützt das äußere Kippmoment. Über Kreuz geführte Direktzurrungen sind daher gegen Kippen der Ladung weniger wirksam als steil geführte.

2.4 Statische Unbestimmtheit komplexer Direktsicherungen

Komplexe Ladungssicherungsanordnungen können aus einer Kombination von Sicherungsmitteln verschiedener Elastizität, unterschiedlicher Abmessungen und unterschiedlicher Wirkrichtungen bestehen. Die Beanspruchung der einzelnen Mittel ist unter diesen Umständen statisch unbestimmt und richtet sich allein danach, wie jedes Sicherungsmittel durch die Bewegung oder Verformung der Ladungseinheit seinerseits verformt wird. Es ist unzulässig, in eine Kräfte- oder Momentenbilanz für jedes dieser Sicherungsmittel die zulässige Belastbarkeit LC einzusetzen. Auf diesen wichtigen Sachverhalt ist bereits im Bericht „Ladungssicherung im Straßenverkehr – Wer kennt die Wahrheit?“ hingewiesen worden.

Dort wurde kurz ein sogenannter selektiver Rechenansatz beschrieben, mit dem das Problem der statischen Unbestimmtheit näherungsweise mit ausreichender Genauigkeit gelöst werden kann. Der selektive Ansatz geht von dem Ladungssicherungsmittel in der betrachteten Anordnung aus, welches in einem bestimmten Lastfall als erstes seine zulässige Belastung erreicht. Diese Belastung wird über die Längenänderung des selektierten Ladungssicherungsmittels in eine Ladungsbewegung/Ladungsverformung umgerechnet. Aus dieser werden die Längenänderungen und Lastaufnahmen aller weiteren Ladungssicherungsmittel bestimmt und einer Bilanz zugeführt. Im folgenden wird dieser Berechnungsweg für die Kräftebilanz in X-Richtung dargestellt.

2.4.1 Unterschiedliche Zurrwinkel und Längen

Werden mehrere Zurrmittel direkt sichernd in unterschiedlichen Winkeln, mit unterschiedlichen Längen und Querschnitten und mit unterschiedlichen Vorspannungen eingesetzt, so muss zunächst das „empfindlichste“ Zurrmittel gefunden werden, welches mit der geringsten Ladungsbewegung seine zulässige Belastung LC erreicht. Da es bei dieser Aufgabe nicht auf letzte Genauigkeit ankommt, werden zur Umrechnung von ΔL in ΔX die vereinfachten Gleichungen (59) verwendet. Mit Gleichung (55) wird zunächst die notwendig Längenänderung ΔL für jedes Zurrmittel bestimmt.

Mit der umgestellten Gleichung (59) erhält man das zugehörige ΔX für jedes der betrachteten Zurrmittel.

Aus den ΔX-Werten wählt man den kleinsten Wert ΔX_min. Die von den übrigen Zurrmitteln aus ΔX_min zu erwartenden Belastungen F_W erhält man dann mit der Gleichung:

Dieser Rechenprozess wird an einem einfachen Beispiel demonstriert. Eine Ladungseinheit ist gegen Rutschen in Fahrtrichtung mit sechs Direktzurrungen gesichert (Bild 37). Diese Zurrungen setzen sich aus drei Typen zusammen, die sich in ihren Komponenten unterscheiden. Als Zurrmittel werden Gurte gewählt mit zulässiger Belastbarkeit LC = 1000 daN und einer nominellen Federkonstanten D_N = 25000 daN. Die Berechnung wird mit einem Tabellenprogramm durchgeführt.

Bild 37: Komplexe Direktzurrung

Die Tabelle in Bild 38 zeigt die Ergebnisse unter der Voraussetzung, dass in allen Gurten die gleiche Vorspannkraft von 400 daN aufgebracht worden ist. Die Laschings vom Typ1 erreichen ihre zulässige Belastung von 1000 daN schon bei einer Längsbewegung der Ladungseinheit von ΔX = 0,055 m. Diese Strecke reicht nur aus, um die Belastung der Laschings des Typs 2 auf 614 daN und derjenigen des Typs 3 auf 697 daN ansteigen zu lassen. Die Sicherungswirkung wird dadurch insgesamt entsprechend eingeschränkt.

Bild 38: Belastungsverteilung bei gleichen Vorspannkräften

Gibt man den Laschings, die als erste die zulässige Belastung erreichen, weniger Vorspannung und den übrigen mehr, so kann die „Ausbeute“ an Sicherungswirkung verbessert werden. In Bild 39 ist das geschehen, allerdings mit der unvermeidlichen Folge, dass die Ladungseinheit unter diesen Umständen eine Strecke von ΔX = 0,077 m rutschen muss, um die Laschings des Typs 1 auf ihre zulässige Belastung von 1000 daN zu bringen. Die übrigen Laschings erreichen mit der etwas höheren Vorspannkraft immerhin rund 80% und 92% ihrer Kapazität.

Bild 39: Belastungsverteilung bei angepassten Vorspannkräften

In Befolgung der Rechenschemata in den gebräuchlichen Richtlinien und Normen hätte man allen drei Typen von Laschings die Belastung LC = 1000 daN zugeordnet.

2.4.2 Unterschiedliche Sicherungsmaterialien

Die parallele Verwendung unterschiedlicher Sicherungsmaterialien, z.B. gleichzeitiges Sichern mit Gurten und Ketten, führt wegen der unterschiedlichen Federkonstanten ebenfalls zu Verlust an Sicherungswirkung. Die nachgiebigeren Sicherungsmittel tragen immer weniger als ihre zulässige Belastbarkeit ermöglichen würde, wenn die steiferen Sicherungsmittel bereits die Grenze ihrer Belastbarkeit erreicht haben.

Besonders drastisch wirkt sich dies aus, wenn eine „steife“ Blockierung mit nachgiebigen Zurrgurten kombiniert wird. Der klassische Fall ist die Sicherung einer schweren Ladung gegen Rutschen nach vorn unter Einbeziehen der Ladeflächenstirnwand.

Die zulässige Belastung von Stirnwänden wird durch die Norm DIN EN 12642:2007 für Standardaufbauten (Code L) mit 0,4 des Gewichts der Nutzlast, aber maximal 5000 daN, und für verstärkte Aufbauten (Code XL) mit 0,5 des Gewichts der Nutzlast gefordert. Die Norm enthält auch eine Angabe über die bei der Typprüfung maximal zulässige elastische Verformung. Diese ist aber sehr allgemein gehalten und erlaubt es nicht, realistische Annahmen über zu erwartende Verformungen einer Stirnwand bei Ausnutzung ihrer zulässigen Belastung zu treffen.

Wird die Stirnwand nur in ihrem unteren Teil belastet, so reagiert sie „unempfindlicher“ und wird sich bei voller Ausnutzung ihrer Kapazität nur im unteren Zentimeterbereich verformen. Bei Belastung über die volle Höhe, die auch einen gewissen Verschub der Ladung voraussetzt, dürfte die zulässige Verformung bereits an den Dezimeterbereich herankommen. Diese Verformung kann als Strecke ΔX_min interpretiert werden und ermöglicht die Abschätzung der Belastung gleichzeitig gesetzter Zurrgurte. Die Gleichung (64) kann für jeden derartigen Gurt oder auch Kette verwendet werden.

Beispiel: Die in Bild 40 dargestellte Sicherungsanordnung kombiniert Niederzurrung, Direktzurrung und Blockierung gegen Rutschen nach vorn. Die Blockierung ist mit Sicherheit die steifste Vorkehrung. Weil die Stirnwand des Fahrzeugs ganz unten beansprucht wird, gibt sie wenig nach. Als Schätzwert für die Verschiebestrecke der Ladung, nach der die Stirnwand bei einer Vollbremsung ihre zulässige Belastung erhält, wird unter Einbeziehen sonstiger Nachgiebigkeiten der Wert ΔX = 0,020 m eingesetzt.

Bild 40: Sicherung in Längsrichtung durch Niederzurrung, Direktzurrung und Blockierung

Mit diesem Schätzwert wird die Wirkung der Längszurrung untersucht. Deren Daten sind: X = 3,0 m, Y = 0,0 m, Z = 1,0 m, L = 3,162 m, LC = 2500 daN, D_N = 62500 daN, F_T = 500 daN. Die genannten Daten gelten auch für die nach hinten gerichtete Direktzurrung. Für beide Laschings wird mit Gleichung (64) die Kraft F_W berechnet, die sich nach einem Versatz der Ladung von ΔX = 0,020 m nach vorn einstellt.

Die Ladungsverschiebung ist so gering, dass die hinten angebrachten Laschings noch nicht kraftlos werden. Die Gesamtsicherungswirkung aller vier Direktzurrungen im Falle einer Vollbremsung ist in vereinfachter Schreibweise mit dem dynamischen Reibbeiwert μ_D = 0,3:

Die Nichtbeachtung der statischen Unbestimmtheit hätte in blinder Befolgung der gebräuchlichen Richtlinien und Normen den beiden vorn angebrachten Direktlaschings jeweils die zulässige Belastung LC zugeordnet und die hinten angebrachten als lose angenommen. Als Gesamtsicherungswirkung hätte sich dann ergeben:

Der Unterschied ist dramatisch, so dass es sehr angebracht erscheint, auf derartige statisch unbestimmte Sicherungsanordnungen in den Richtlinien und Normen in geeigneter Weise(9) einzugehen.